Content uploaded by Françoise Ochsenbein
Author content
All content in this area was uploaded by Françoise Ochsenbein on Mar 02, 2015
Content may be subject to copyright.
Journal of Biomolecular NMR, 19: 3–18, 2001.
KLUWER/ESCOM
© 2001 Kluwer Academic Publishers. Printed in the Netherlands.
3
15
N NMR relaxation as a probe for helical intrinsic propensity: The case of
the unfolded D2 domain of annexin I
F. Ochsenbein
∗,∗∗
,R.Guerois
∗∗∗
,J.-M.Neumann
∗
,A.Sanson
∗
, E. Guittet & C. van Heijen-
oort
∗∗∗∗
CNRS, Institut de Chimie des Substances Naturelles, 1 avenue de la terrasse, F-91190 Gif sur Yvette, France
Received 7 July 2000; Accepted 13 November 2000
Key words: annexin, dynamics,
15
N NMR relaxation, protein folding, unfolded state
Abstract
The isolated D2 domain of annexin I is unable to adopt a tertiary fold but exhibits both native and non-native
residual structures. It thus constitutes an attractive model for the investigationof dynamics of partially folded states
in the context of protein folding and stability.
15
N relaxation parameters of the D2 domain have been acquired
at three different magnetic fields, 500, 600 and 800 MHz. This enables the estimation of the contribution of
conformational exchange to the relaxation parameters on the micro- to millisecond time scale, thus providing
a suitable data set for the description of motions on the pico- and nanosecond time scale. The analysis of the
seven spectral densities obtained (J(0), J(50 MHz), J(60 MHz), J(80 MHz), <J(500 MHz)>,<J(600 MHz)>,
<J(800MHz)>) providescomplementaryand meaningfulresults on the conformationalfeatures of the D2 domain
structure previously depicted by chemical shift and NOE data. Especially, residual helix segments exhibit distinct
dynamical behaviors that are related to their intrinsic helical propensity. Beside the spectral density analysis, a
series of models derived from the Lipari and Szabo model-free approach are investigated. Two models containing
three parameters are able to reproduce equally well the experimental data within experimental errors but provide
different values of order parameters and correlation times. The inability to find a unique model to describe the data
emphasizes the difficulty to use and interpret the model-free parameters in the case of partially or fully unfolded
proteins consisting of a wide range of interconverting conformers.
Abbreviations: CD, circular dichroism; CPMG, Carr, Purcell, Meiboom and Gill; CSA, chemical shift anisotropy;
DSS, 2,2-dimethyl-2-silapentane-5-sulfonic acid; EDTA, ethylene-diamide-tetra-acetic acid; FID, free induction
decay; MD, molecular dynamics; NOE, nuclear Overhauser effect; R
N
(N
z
), longitudinal
15
N relaxation rate
constant; R
N
(N
x,y
), transverse
15
N relaxation rate constant; R
N
H
N
z
↔ N
z
, cross-relaxation rate between amide
proton and nitrogen.
Introduction
Annexins constitute a family of multi-domain proteins
characterized by a main C-terminal core whose three-
∗
Present address: D
´
epartement de Biologie Cellulaire et
Mol
´
eculaire, Section de Biophysique des Prot
´
eines et des
Membranes, CEA de Saclay and URA CNRS 2096, F-91191 Gif
sur Yvette Cedex, France.
∗∗
F. Ochsenbein and F. Cordier-Ochsenbein refer to the same
author.
∗∗∗
Present address: Structural Biology program, EMBL, Meyer-
hofstrasse 1, D-69117 Heidelberg, Germany.
dimensional organization is highly hierarchical. This
core consists of four ∼70-residue domains, D1 to D4
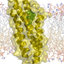
(Figure 1a), exhibiting an identical topologywith only
a limited sequence homology of approximately 30%.
The domain topology comprises five helix segments,
named A to E (Figure1b), organizedin a characteristic
super-helix motif (Huber et al., 1992; Bewley et al.,
1993; Concha et al., 1993; Weng et al., 1993).
∗∗∗∗
To whom correspondence should be addressed. E-mail:
carine@icsn.cnrs-gif.fr
4
Nt
Ct
A
D
D3
E
D1
b)
D4
D2
B
C
a)
Nt
Ct
Figure 1. (a) Ribbon representation of the structure of annexin I
from crystallographic data (top view). (b) Ribbon representation of
the structure of annexin I D2 domain from crystallographic data
(side view), showing the five helices of the consensus annexin
topology. These figures were drawn using the Molscript program
(Kraulis, 1991).
Recently, several results using CD and NMR spec-
troscopy have revealed that, when isolated from the
rest of the protein, the annexindomains exhibit a large
scale of stability. In particular, we have shown that the
isolated D1 domain of annexin I conserves the super-
helix 3D topology, thus constituting an autonomous
folding unit. In contrast, the D2 domain is unable
to adopt a tertiary fold, exhibiting only residual sec-
ondary structures (Cordier-Ochsenbein et al., 1996,
1998a, b). These findings justify our choice of an-
nexins as suitable models for investigating the mecha-
nisms governingthe folding process of a multi-domain
protein and the sequence–stability relationships asso-
ciated with a given topology.
Previous
1
H-
15
N NMR conformational analysis
has shown that the residual structure of the iso-
lated D2 domain of annexin I comprises both native
and non-native secondary structure elements (Cordier-
Ochsenbein et al., 1998a). The native elements consist
of four helix segments corresponding to the B and E
helices as well as to a large proportion of the A he-
lix and a small helix population corresponding to the
second part of the C helix. The region corresponding
to the D helix is found to be almost fully disordered.
The non-nativestructures comprise a cappingbox pre-
venting the stabilization of the complete nativeA helix
(Guerois et al., 1998) and a set of inter-converting
turn-like structures preventing the formation of the
remaining elements of the native C helix. An essen-
tial feature is that most of the key residues forming
the non-native local structures are involved in var-
ious inter-domain long-range interactions stabilizing
the nativestructureof the whole protein. All these con-
siderations point to the D2 domain as obviously rich
in information in the context of protein folding and
stability. Moreover, it should be emphasized that the
residual structures of the D2 domain, both native and
non-native, are spontaneously formed in pure aqueous
solution, i.e. in the absence of denaturing agents.
The residual structures described above are highly
flexible with one or few conformations, which are
favored among a wide range of inter-converting con-
formers. Information about the dynamics of the resid-
ual structures is needed to fully characterize the par-
tially folded state of the domain.
15
N NMR relaxation
studies provide suitable sets of data for investigat-
ing protein backbone dynamics, and this approach
has been reported in several publications devoted to
partially folded proteins (Alexandrescu and Shortle,
1994; Frank et al., 1995; Buck et al., 1996; Brutscher
et al., 1997; Farrow et al., 1997; Schwalbe et al.,
1997; Dyson and Wright, 1998; Eliezer et al., 1998;
Meekhof and Freund, 1999). In the case of the D2
domain, we have investigated how native and non-
native secondary structures influence the time scale
of the predominant local fluctuations of the backbone
and how they can be distinguished by their dynamical
behavior.
We performed
15
N relaxation experiments on the
D2 domain at three different magnetic fields, 500,
600 and 800 MHz, which allowed us to determine
values of the spectral density function at seven fre-
quencies (J(0), J(50 MHz), J(60 MHz), J(80 MHz),
<J(500 MHz)>, <J(600 MHz)>, <J(800 MHz)>).
The evolution of these spectral densities along the
5
D2 domain sequence providesmeaningfulinformation
on the dynamical behavior of the protein, which is
compared with the conformational features previously
depicted by chemical shifts and NOE data (Cordier-
Ochsenbein et al., 1998a). The most striking result is
the correlation found between the dynamical features
of residual helical segments and their intrinsic helical
propensity.We show that residual helices stabilized by
local interactions are characterized by a lower flexibil-
ityin the sub-nanosecondrangeas compared to helices
stabilized by long-range interactions. In order to ob-
tain motional parameters, a model-free analysis has
been performed. We showthatthis approach yields ap-
parent order parameters and discrete correlation times
whose interpretation is problematic in the context of
unfolded proteins. Finally, the reduced spectral den-
sity analysis is the most relevant approach to analyze
the dynamical features of the unfolded D2 domain.
Materials and methods
NMR sample
TheannexinI D2domainwas cloned, overproducedas
a uniformly
15
N-labeled sample, and purified as pre-
viously described (Cordier-Ochsenbein et al., 1995,
1998b). All experiments were performed at 35
◦
Con
a1mM
15
N-labeled protein sample in solution in
a 35 mM perdeuterated Tris buffer, 200 mM NaCl,
0.1 mM EDTA, 1 mM NaN
3
, 0.1 mM DSS and 10%
D
2
OatpH= 6.0.
NMR experiments
NMR experiments were carried out on Bruker DRX
spectrometersoperating at 500, 600 and 800 MHz and
equipped with 5 mm triple-resonance gradient probes
with actively shielded three axis gradients.
The pulse sequences used to determine
15
N
R
N
(N
z
), R
N
(N
x,y
)and
1
H-
15
N NOEs were based on
those previously described (Farrow et al., 1994) with
minor modifications. The monitoring of water mag-
netization is particularly important when dealing with
unfolded proteins whose amide protons are in fast ex-
changewith the solvent. Special care was thus taken to
avoid exchange effects. Gradient pulses were inserted
during the relaxation delay in R
N
(N
z
) experiments in
order to avoid radiation damping and thus to ensure
that most of the water magnetization lies on the +z
axis just before acquisition. A CPMG sequence was
used for the measurement of R
N
(N
x,y
) with a 1 ms
delay between the
15
N 180
◦
pulses.
15
N decoupling
during acquisition was performed using a GARP se-
quence (Shaka et al., 1985). All experiments were
recorded with the
15
N sweep-width set to 25 ppm,
and the
1
H sweep-width to 3.0 ppm with the carrier
set to the center of the amide proton resonances. Each
2D data set consisted of 1024 complex data points in
t
2
and 100 complex points in t
1
. Twenty-four scans
were acquired per free induction decay, except for the
NOE measurements, which used 96 scans due to the
lack of an initial polarization transfer. In all cases,
quadrature detection was achieved by the TPPI-States
method (Marion et al., 1989). A WATERGATE on-
resonance sequence was used just prior to acquisition
to suppress the solvent resonance (Piotto et al., 1992).
For the heteronuclear
1
H-
15
N NOEs, a carefully
optimized water flip-back pulse was added before the
last proton 90
◦
pulse in the experimentwithout satura-
tion (Grzesiek and Bax, 1993). The two experiments
with and withoutprotonsaturation were acquiredin an
interleaved manner,FID by FID. A relaxation delay of
10 s was used before the FID of the experiment with-
out saturation. The power used for proton saturation
was optimized in a 1D experiment in order to min-
imize the heating of the sample. A GARP sequence
with proton pulses at a power of ∼1 W applied during
4 s was sufficient to reach the
1
H-
15
N heteronuclear
NOE steady state.
For the other experiments, a recycle delay of
4 s was employed. R
N
(N
z
) values were obtained at
500 MHz with 13 delays of 12, 24, 48, 72, 96, 156,
180, 240, 324,396, 540, 696and 1020ms, at 600MHz
with 8 delays of 12, 48, 96, 180, 300, 480, 696 and
1020 ms and at 800 MHz with 11 delays of 12, 48,
72, 96, 180, 240, 396, 540, 696, 1020 and 2000 ms.
R
N
(N
x,y
) values were obtained at 500 MHz with 12
delays of 8, 24, 48, 64, 80, 144, 200, 280, 344, 400,
496 and 800 ms, at 600 MHz with 8 delays of 8, 24,
48, 80, 144, 200, 400 and 496 ms and at 800 MHz
with 10 delays of 8, 24, 32, 48, 80, 144, 200, 280, 400
and 496 ms. In all these experiments, the points corre-
sponding to different relaxation delays were acquired
in an interleaved manner to avoid any bias that could
arise from long-term instabilities.
Data processing and determination of relaxation
rates
NMR spectra were processed using the GIFA soft-
ware (Pons et al., 1996). A pure cosine bell and a
pure squared cosine bell were applied along t
1
and t
2
,
respectively. The data were zero-filled to 512 points
along t
1
and to 2048 points along t
2
prior to Fourier
6
transform. Finally, a baseline correctionwas applied in
both dimensions using the corresponding GIFA base-
line routine (Rouh et al., 1993). Cross-peak intensities
were determined from peak heights using the GIFA
peak-picking routine. Relaxation rate determination
and error estimation were performed as already de-
scribed (Palmer III et al., 1991; Mandel et al., 1995).
The fitting to a mono-exponential decay was achieved
using the non-linear Levenburg–Marquardtminimiza-
tion algorithm (Press et al., 1988) implemented in
the MATLAB software. All the fitting procedures
were written using this software. The goodness of
fits and error estimations were obtained using estab-
lished Monte Carlo procedures, with an experimental
Gaussian error set to 5% of the experimental inten-
sities and using a set of 500 synthetic data for each
N-H vector. NOE enhancements were obtained as the
ratio of the peak heights in the spectra recorded with
and without saturation of protons during the relax-
ation delay. The uncertainties of these NOEs were
the sum of the uncertainties of the peak intensities in
each experiment.The crossrelaxationrate between the
amide proton and nitrogen R
N
(H
N
z
↔ N
z
) was then
calculated according to the following expression:
NOE = 1 +
γ
H
γ
N
R
N
(H
N
z
↔ N
z
)
R
N
(N
z
)
(1)
Analysis of relaxation data
Measured NMR
15
N relaxation parameters are related
to the motions of the
1
H-
15
N vectorthroughtheir spec-
tral densities at the five frequencies: 0, ω
N
, ω
H
+ω
N
,
ω
H
and ω
H
−ω
N
. These spectral densities give the
proportion of the energy used for the motions at the
correspondingfrequencies.
Evaluation of conformational exchange from
measurements at three fields
We exploited the quadratic dependence of the ex-
change contribution to
15
N transverse relaxation in
the fast exchange limit and the relationship between
R
N
(N
x,y
)andR
N
(N
z
) (Phan et al., 1996). Using
the standard expression for these relaxation rates as
functions of the spectral densities and the exchange
contribution, one can write:
R
N
(N
z
) −
R
N
(N
x,y
)
2
=
6d + 2c
3
J(0)
+3dJ(ω
H
) + R
ex
(2)
where d is the strength of the dipolar interactions
between the amide nitrogen and proton and c is the
strength of the chemical shift anisotropy. These con-
stants are given by
d =
µ
0
4π
2
¯
h
2
γ
2
H
γ
2
N
4r
6
H
N
N
c =
ω
2
N
δ
2
CSA
3
(3)
where µ
0
is the vacuum permeability,
¯
h Planck’s con-
stant divided by 2π and γ the gyromagnetic ratio
(γ
H
= 2.6752 × 10
8
s
−1
T
−1
and γ
N
=−2.711 ×
10
7
s
−1
T
−1
). For a magnetic field of 14.1 Tesla, an
internuclear distance
15
N-
1
H bond r
H
N
N
of 0.102 nm
and a chemical shift anisotropy δ
CSA
of −172 ppm,
d = 1.2986 × 10
9
s
−2
and c = 1.439 × 10
9
s
−2
at
600 MHz.
For an exchange contribution R
ex
> 1s
−1
,
3dJ(ω
H
) can be reasonably neglected in the second
term of the equation, which can then be rearranged as:
R
N
(N
z
) −
R
N
(N
x,y
)
2
=
2c
1
3
J(0)
+A
ex
B
2
0
+ 2dJ(0) (4)
where c
1
is equal to c/B
2
0
.ThevalueofJ(0) can
then be obtained from the intercept of the plot of
{R
N
(N
z
)−R
N
(N
x,y
)/2} versusB
2
0
. The exchangecon-
stant A
ex
can be calculated from the slope of the line.
Any spin for which the slope is higher than 2c
1
J(0)/3
has an exchange contribution A
ex
B
2
0
to its transverse
relaxation rate. The uncertainties in the values of A
ex
were obtained from Monte Carlo procedures similar
to those described for the relaxation rates evaluation.
The fits were statistically relevantfor all residues, with
a mean value of χ
2
exp
equal to 0.09 ± 0.2 and of χ
2
95
equal to 3.7 ± 0.6.
Spectral density calculation
Spectral densities J(ω) were calculated using the re-
duced matrix approach proposed by Peng and Wagner
and co-workers (Peng and Wagner, 1992a, b; Farrow
et al., 1995a;Lefevreet al., 1996; vanHeijenoortetal.,
1998) with values of c and d given in Equation 3. We
used a value of 0.102 nm for r
H
N
N
and a chemical
shift anisotropy δ
CSA
of −172 ppm. Indeed,these val-
ues have beenrecently shown to be more accuratethan
thoseused inthe majorityof previousstudies(r
H
N
N
of
0.102nm and δ
CSA
of−160 ppm)(Boydand Redfield,
1999; Ishima and Torchia, 2000). This approach en-
ables the accurate calculation of the spectral densities
at frequencies 0 and ω
N
and the evaluation of a spec-
tral density <J(ω
H
)> at high frequency. <J(ω
H
)>
is close to J(ω
H
+ ω
N
)orJ(0.85ω
H
) (Farrow et al.,
1995b; Ishima et al., 1995; Ishima and Nagayama,
7
1995; Peng and Wagner, 1995). In this treatment, J(0)
includes the exchange contribution from R
N
(N
x,y
)
which depends on the field. Nine values of the spectral
density were thus obtained. In order to analyze only
fast motions ranging from the pico- to the nanosecond
time, J(0) without the contribution of slow exchange
was obtained for each magnetic field using the value
of (R
N
(N
x,y
)−R
ex
), where R
ex
is the contribution of
conformational exchange previously determined.
Evaluation of motion parameters
Direct analysis of the spectral densities providesa pic-
ture of the distribution of the frequencies of N-H bond
motions along the protein backbone. However, extrac-
tion of more pictorial informationabout motions, such
as correlation times and amplitudes, requires the use
of models and thus the formulation of hypotheses on
motions. A usual assumption is to consider that the
segmental motions of N-H or C-H bonds in a protein
are not correlated, so that the correlation function and
thus the spectral density function can be decomposed
into a weighted sum of contributions:
J(ω) = a
0
J
0
(ω) +
X
i>0
a
i
J
i
(ω) (5)
where the first term a
0
J
0
(ω) represents the overall
tumbling of the protein, and
P
i≥0
a
i
= 1.
Among the various models derived from this equa-
tion, the model-free approach proposed by Lipari and
Szabo (1982a,b), and its subsequently extended ver-
sion proposed by Clore et al. (1990a,b) are the most
widely used. The expression of the spectral density
correspondingto the initial model of Lipari and Szabo
containing two correlation times is given by:
J(ω) =
2
5
"
S
2
τ
c
1 + (ωτ
c
)
2
+
(1 − S
2
)τ
0
i
1 + (ωτ
0
i
)
2
#
,
1
τ
0
i
=
1
τ
c
+
1
τ
i
(6)
where τ
i
is the effective correlation time for internal
motions.
The expression for the spectral density function in
the extended version of the model is the sum of three
Lorentzians and is given by:
J(ω) =
2
5
"
(S
2
f
S
2
s
)τ
c
1 + (ωτ
c
)
2
+
S
2
f
(1 − S
2
s
)τ
0
s
1 + (ωτ
0
s
)
2
+
1 − S
2
f
)τ
0
f
1 + (ωτ
0
f
)
2
#
,
(7a)
with
1
τ
0
s
=
1
τ
c
+
1
τ
s
and
1
τ
0
f
=
1
τ
c
+
1
τ
f
(7b)
The first term of the equation is related to the slowest
motion and is weighted by the square of a generalized
order parameter for internal motions S
2
= S
2
f
S
2
s
· S
2
,
S
2
f
and S
2
s
provide a model-independent measurement
of the spatial restriction of, respectively, all, fast (on
the picosecondtime scale) and slow (around 1 ns) time
scale internal motions. S
2
f
and S
2
s
are associated with
two effective correlation times, respectively, τ
f
and
τ
s
.
In Equations 6 and 7, the highest correlation time
τ
c
was considered, either as an overall tumbling corre-
lation time τ
R
, and was then identical for all residues,
or as a local correlation time, and was thus fitted on
a per residue basis. Models considering an overall
tumbling correlation time were named MF (for model-
free), those fitting τ
c
on a per residue basis were
named LMF (for local model-free); they are listed in
Table 1. Models are indexed according to the number
of adjustable parameters.
Goodness of fits and uncertainty evaluation
J(ω) in Equations 6, 7a and 7b is a function of
one to five unknown variables that can theoretically
be evaluated from the nine independently measured
relaxation parameters at the three fields. Additional
exchange broadening contributions to transverse re-
laxation parameters R
N
(N
x,y
) obtained as described
abovewere removed from the experimentalvalues. No
exchange contribution was thus taken into account in
all described fits.
Motion parameters were optimized for each
residue for which the data could be collected from
non-linear least-squares minimization of the error
function χ
2
exp
:
χ
2
exp
=
X
all
frequencies
"
R
N
(N
x,y
)
calc
− R
N
(N
x,y
)
exp
δR
N
(N
x,y
)
2
+
R
N
(N
z
)
calc
− R
N
(N
z
)
exp
δR
N
(N
z
)
2
+
NOE
calc
− NOE
exp
δNOE
2
#
(8)
where δ(X) (X being R
N
(N
x,y
), R
N
(N
z
)orNOE)
is the estimated experimental error of the relaxation
parameters. The subscripts exp and calc refer to ex-
perimental and back-calculated relaxation parameters,
respectively. Initial values for parameters were ob-
tained from a grid search minimization. The goodness
8
0 10203040506070
0 10203040506070
J(0) (ns) (without R
ex
) J(0) (ns)
0 10203040506070
J(ω
N
) (ns)
0
0.5
1
1.5
2
2.5
0
0.5
1
1.5
2
2.5
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0
0.01
0.02
0.03
0.04
0.05
0 10203040506070
<J(ω
H
)> (ns)
A
BC E
A
BC E
sequence
(a)
(b)
(c)
(d)
Figure 2. Values of the spectral density function (in ns) determined for the D2 domain at pH 6 and 35
◦
C from
15
N relaxation data performed at
500 MHz (filled circles), 600 MHz (open diamonds) and 800 MHz (filled triangles) as a function of the domain sequence. (a) At zero frequency
including the contribution of conformational exchange. (b) At zero frequency after subtraction of the exchange contribution. (c) At frequency
ω
N
(50, 60 and 80 MHz) and (d) at frequency 0.85 ω
H
(435, 522 and 696 MHz). Bars represent the experimental error. Boxes at the top of the
figure delineate the residual helices, gray boxes delineate the non-native turn-like structures.
9
Table 1. Parameters corresponding to the various models used to fit the experimental
NMR relaxation parameters
Approach
a
Model
b
Optimized parameters Fixed parameters
Model free with one LMF
1
τ
c
none
time scale
Model free with two time MF
1
S
2
τ
R
, τ
i
scales (Equations 6 and 7) MF
2
S
2
, τ
i
τ
R
LMF
2
τ
c
, S
2
τ
i
LMF
3
τ
c
, S
2
, τ
i
none
Model free with three time MF
3
S
2
f
, S
2
s
, τ
s
τ
R
, τ
f
scales (Equations 6 and 7) MF
4
S
2
f
, S
2
s
, τ
s
, τ
f
τ
R
LMF
4
S
2
s
, S
2
f
, τ
c
, τ
s
τ
f
LMF
5
S
2
s
, S
2
f
, τ
c
, τ
s
, τ
f
none
a
Each approach corresponds to the indicated general expression of the spectral density
function.
b
LMF stands for a local version of the model-free approach, in which the highest cor-
relation time, τ
c
is fitted on a per residue basis. MF refers to a model-free version in
which the highest correlation time corresponds to the overall tumbling of the molecule
τ
R
and is thus identical for all residues. Models are referenced according to the number
of optimized parameters.
of the fits and the uncertainties were obtained from
statistical analysis (Palmer III et al., 1991; Mandel
et al., 1995). Five hundred simulated data sets were
selected from a Gaussian noise distribution centered
on the relaxation rates back-calculated from the opti-
mized parameters and correspondingto the previously
estimated errors in experimental R
N
(N
x,y
), R
N
(N
z
)
and NOEs. A model was considered satisfactory if the
optimized χ
2
exp
lay within the 95% confidence limit
obtained from the 500 Monte Carlo simulations, i.e.
χ
2
exp
< χ
2
95%
. The uncertainties in the values of the
model-free parameters were the standard deviation of
the simulated parameters.
Results
NMR relaxation parameters and spectral densities
We determined the R
N
(N
z
), R
N
(N
x,y
)and
1
H-
15
Nhet-
eronuclearNOE relaxation parameters of 56 out of the
71 amide nitrogen nuclei of the domain at three differ-
ent magnetic field strengths, 500, 600 and 800 MHz
(data not shown). As expected for a partially folded
domain, most of the
1
H-
15
N heteronuclear NOEs do
not exceed 0.5, instead of the average value of 0.8
usually found for folded proteins of a similar size.
Following the reduced density matrix formalism
(Peng and Wagner, 1992a, b; Farrow et al., 1995a;
Lefevre et al., 1996; van Heijenoort et al., 1998), val-
ues of the spectral density function have been derived
from the relaxationparameters at three frequencies for
each magnetic field: J(0), J(ω
N
), <J(ω
H
)>,where
<J(ω
H
)> is close to J(ω
H
+ ω
N
)orJ(0.85 ω
H
)
(Farrow et al., 1995b; Ishima et al., 1995; Ishima
and Nagayama, 1995; Peng and Wagner, 1995). This
analysis enabled us to determine the value of J(ω)for
seven differentfrequencies:0, 50, 60, 80, 435, 522and
696 MHz. Results are reported in Figure 2 (panels a,
c and d). As expected, the spectral density obtained
for each residue is a monotonically decreasing func-
tion of the frequency. Moreover, the variations of the
spectral densities along the domain sequence are re-
markably conserved for the three fields, showing the
consistency of the data. Five residues (26, 27, 40, 45
and 54) show large differences between the values of
J(0) at the three fields, characteristic of the presence
of conformational exchange in the µs-ms range. Its
contribution to the relaxation data can be accurately
evaluated as proposed by Phan et al., exploiting its
anticipated quadratic field dependence: R
ex
= A
ex
B
2
0
,
where B
0
is the magnetic field strength and A
ex
is a
constant (Phan et al., 1996). A
ex
was estimated for
each residue from the linear regression of the curve
{R
N
(N
x,y
)−R
N
(N
z
)/2} versus B
2
0
(see Materials and
methods). Figure 3 shows the exchange contribution
R
ex
for the three field strengths as a function of the
10
0
2
4
6
8
10
12
14
16
010203040506070
R
exch
(s
-1
)
0
4
8
12
0 100 200 300 400
R
N
(N
x,y
)-R
N
(N
z
)
0
2
(T
2
)
B
/2 (s
-1
)
A'
B' C' E'
A
BC E
sequence
Figure 3. Contribution of the conformational exchange parameter (R
ex
)tothe
15
N transverse relaxation of the D2 domain at three field
strengths, 500 MHz (filled circles), 600 MHz (open diamonds) and 800 MHz (filled triangles) as a function of the D2 domain sequence. Bars
represent the standard deviation of simulated parameters. Insert: plot of {R
N
(N
x,y
) − R
N
(N
z
)/2} versus B
2
0
for the experimental determination
of the conformational exchange contribution R
ex
for several residues. For each residue, experimental values are represented by the following
symbols: A
10
, filled circles; L
26
, open squares; D
60
, filled triangles. Bars represent the experimental error and thick lines the linear regression
of each data set. Boxes at the top of the figure delineate the residual helices, gray boxes delineate the non-native turn-like structures.
0.001
0.01
0.1
1
10
J(τ
c
) (ns)
τ
c
(ns)
02468
ω=0
ω=60 MHz
ω=540 MHz
J
exp
(60 MHz)
J
exp
(0)
J
exp
(540 MHz)
0246810
ω=0
ω=60 MHz
ω=540 MHz
τ
c
(ns)
J
exp
(60 MHz)
J
exp
(0)
J
exp
(540 MHz)
J(ω
H
+ω
N
)
1
J(ω
N
)
1
J(ω
H
+ω
N
)
1
J(ω
N
)
1
Figure 4. Theoretical values of the spectral densities J(0), J(ω
N
)and<J(ω
H
)> at 600 MHz as a function of the correlation time τ
c
assuming
a unique isotropic motion (thin continuous curves) compared with the experimental spectral densities obtained for the N-terminal segment 5–51
(left panel) and the C-terminal 52–68 segment (right panel) of the D2 domain at 600 MHz. The dispersion of experimental spectral density
values J(0), J(ω
N
)and<J(ω
H
)> is represented by horizontal gray bars. The mean experimental values of J(0), J(ω
N
)and<J(ω
H
)> are
represented as horizontal dotted lines. The segments of the theoretical curves that match the experimental values are thickened. Vertical bars
indicate the position of the maximum of the theoretical curves of J(ω
N
)and<J(ω
H
)>. These two limits delineate the range of correlation
times where the variations of J(ω
N
)and<J(ω
H
)> are anti-correlated.
11
sequence. The plot of {R
N
(N
x,y
)−R
N
(N
z
)/2} versus
B
2
0
is reported for several residues. Remarkably, the
contribution of conformational exchange is relatively
weak, less than 3 s
−1
except for the five residues men-
tioned above (26, 27, 40, 45 and 54). In order to
analyzeonly fast motionsrangingfromthe pico- tothe
nanosecond time scale, the contribution of slow con-
formational exchange was subtracted from the values
of J(0) obtained from the relaxation data at 500, 600
and 800 MHz (see Materials and methods, Figure 2b).
As expected, the resulting profiles no longer exhibit
the oscillations previously observed. The relaxation
data obtained at each magnetic field lead to identical
values of J(0) within the experimental error (see Fig-
ure 2b). This result confirms the reliability of the data.
In the following, the expression J(0) will refer to the
spectral density function without the slow exchange
contribution.
The comparison of the spectral density values ob-
tained for the D2 domain with theoretical values of
J(0), J(ω
N
)and<J(ω
H
)> corresponding to a unique
isotropic motion allows a first estimation of the time-
scale of the motions that mainly contribute to the
loss of correlation of NH bond orientations. These
theoretical values J(0), J(ω
N
)and<J(ω
H
)>, calcu-
lated for a magnetic field of 14.1 Tesla (600 MHz),
are plotted as a function of correlation time in fig-
ure 4. The experimental values of J(0), J(ω
N
)and
<J(ω
H
)> obtained for the N-terminalsegment(5–51)
and for the C-terminal segment (52–68) are reported
in Figure 4 in the left and right panel, respectively.
For these two segments, values of J(0) range from
0.2 to 1 ns. They are smaller than those expected
for a folded protein of this size. This indicates that
the decay of the auto-correlation function is mainly
due to motions below 2.5 ns (estimated from J(0) =
2τ
c
/5). This is corroborated by the rather flat shape
of the spectral density along the frequency dimen-
sion. The increase (decrease) of J(ω
N
) is compensated
by a decrease (increase) of <J(ω
H
)> along the do-
main sequence at the three fields (Figure 2). This
anti-correlation indicates that motions mainly occur
between 1/(ω
H
+ ω
N
) and 1/ω
N
(Figure 4). It thus
allows the evaluation of a lower limit of the correlation
times around 1/(ω
H
+ ω
N
) (180 ps at 800 MHz) and
an upper limit around 1/ω
N
(3.2 ns at 500 MHz). Al-
together, the decay of the auto-correlation function is
mainly due to motions between 180 ps and 2.5 ns. The
segments of the theoretical curves of spectral densities
that match the experimental values are thickened in
Figure 4, highlighting the ranges of correlation times
compatible with the experimental data. It should be
noted that these ranges of τ
c
do not strictly coincide
for all spectral densities, indicating that the dynam-
ics of the domain can not be described by a unique
isotropic motion.
Considering the variation of the spectral densities
along the D2 domain sequence, the values are not
uniform, showing that different dynamical behavior
occurs along the domain backbone(Figure2, panels b,
c and d). Except for the residues located at the N-
and C-terminal extremities (1–3 and 69–71), which
show as expected the lowest values of J(0)andJ(ω
N
)
and the highest values of <J(ω
H
)>, two regions can
be distinguished in the domain: the N-terminal seg-
ment (5–51) and the C-terminal segment (52–68). In
the (5–51) segment (Figure 4, left panel), the average
values of J(0)andJ(ω
N
) are found to be higher than
those in the (52–68) segment (Figure 4, right panel)
and the average value of <J(ω
H
)> is found to be
lower. Altogether, these results indicate that on aver-
age, the (5–51) segment exhibits a lower flexibility in
the sub-nanosecond range than the (52–68) segment.
In the N-terminal (5–51) segment, the fluctuations
of J(ω
N
)and<J(ω
H
)> are remarkably correlated
with the residual secondary structures indicated as
boxes at the top of Figure 2. Higher values of J(ω
N
)
and lower values of <J(ω
H
)> are observed in the
segments correspondingto the A, B and C residual he-
lices. In contrast, in the (52–68) C-terminal segment,
the shape of J(ω
N
)and<J(ω
H
)> is rather flat and the
residual E helix (60–70) exhibits values of J(ω
N
)and
<J(ω
H
)> close to those of the completely unfolded
(50–58) segment.
Model-free analysis
The capability of the model-free approach to correctly
reproduce the experimental data and to provide phys-
ically relevant motional parameters was then investi-
gated. We used various formalisms of the model-free
approach, differing by the number of distinct correla-
tion times they contain, and by the physical meaning
of the highest correlation time (either overall tumbling
or segmental motion). The characteristics of the dif-
ferent models are fully commented in Table 1 and in
the Materials and methods section. For the sake of
clarity, results are presented following the number of
independent correlation times included in the models.
As expected from the previous spectral density
analysis, model LMF
1
(LMF
1
standsfor Local Model-
Free containing one adjustable parameter) comprising
a unique adjustable correlation time τ
c
is not able to
12
0 10203040506070
0 10203040506070
0 10203040506070
0.5
1
1.5
2
2.5
3
3.5
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0
5
10
15
20
0 10203040506070
τ
c
(ns)
S
2
sequence
χ
2
τ
i
(ns)
A
BC E
A
BC E
(a)
(b)
(c)
(d)
Figure 5. ‘Local model-free’ parameters derived from
15
N relaxation measurements obtained for the D2 domain at pH 6 and 35
◦
Cusingthe
LMF
3
model (see Table 1) as a function of the domain sequence. (a) Local correlation time τ
c
. It is fitted on a per residue basis and accounts for
the slowest effective rotational motion in the nanosecond range. (b) Generalized order parameter S
2
corresponding to the internal correlation
time τ
i
. (c) Internal correlation time τ
i
. (d) The fit is considered as satisfactory if χ
2
exp
is ranged within the 95% confidence limit χ
2
95%
(open
circles) obtained from 500 Monte Carlo simulations, i.e. χ
2
exp
< χ
2
95%
. Boxes at the top of the figure delineate the residual helices, gray boxes
delineate the non-native turn-like structures.
13
reproduce experimental data within experimental er-
ror (data not shown). Relaxation data have then been
fitted with models including two distinct correlation
times. In this case, the slowest motion either repre-
sents the overall tumbling of the molecule and is thus
characterized by a unique value τ
R
(MF
1
,MF
2
,see
Table 1), or is adjusted on a per residue basis (LMF
2
,
LMF
3
, see Table 1). Fitting experimental data with
models MF
2
and LMF
2
does not provide satisfac-
tory results according to statistical criteria (data not
shown). Model LMF
3
yields statistically acceptable
results for all residues but three (residues 27, 34 and
44) (Figure 5). As for the spectral density analysis, the
values of τ
c
along the protein sequence lead us to dis-
criminate two specific behaviors: that of the segment
5–51 (τ
c
= 2.4 ± 0.4 ns) and that of the segment 52-
68 (τ
c
= 1.57 ± 0.3 ns). As expected, the residues
located at the N and C extremities show the lowest
value of correlation time (τ
c
= 1 ns). Values of the
order parameters S
2
remain smaller than 0.60 along
the whole sequence, suggesting a large contribution
of fast internal motions to the loss of correlation of
the NH bond orientations.The associated time scale is
about 80 ps, as indicated by the τ
i
values.
Recent studies showed that more than two time
scales are often needed to characterize the dynami-
cal behaviorof partially folded proteins(Alexandrescu
and Shortle, 1994; Brutscher et al., 1997; Orekhov
et al., 1999). We have thus fitted our experimental data
using models including three time scales of motion
(seeTable 1 and Equation7). As previously, the largest
correlationtime is either consideredas a uniqueglobal
correlation time (MF
3
,MF
4
) or fitted on a per residue
basis (LMF
4
,LMF
5
). Models including more than
three adjustable parameters (MF
4
,LMF
4
and LMF
5
)
lead to erratic profiles of the fitted parameters along
the domain sequence and, for several residues, to un-
realistic values of fitted parameters as, for example,
nearly null values of orderparameters or unreasonably
high values of correlation times (> 50 ns) (data not
shown). Even a careful adjustment of initial conditions
performed by grid search analysis does not improve
the fittings. The three different correlation times that
are considered in these models have probably values
that are too close and therefore do not correspond to
uncorrelated motions as it is assumed by the formal-
ism. Moreover, slight variations of the data within
the experimental error lead to divergent values of the
fitted parameters, indicating that the corresponding
uncertainties are very large.
As a result, the only reliable model containing
three distinct correlation times is the MF
3
model. The
value of the overall tumbling correlation time τ
R
has
been determined according to the following consid-
erations. In the case of folded proteins, an initial
estimation of τ
R
is usually derived from the mean
value of the R
N
(N
x,y
)/R
N
(N
z
) ratios averaged over
the residues located in the most structured segments
of the protein (Kay et al., 1989). Residues exhibiting
either conformational exchange or significant internal
motions (NOEs < 0.65) are excluded. In our case,
all heteronuclear NOEs are less than the critical value
of 0.65 and this procedure is thus inapplicable. For a
fully folded domain of the size of D2, the overall cor-
relation time is expected to be around 4 ns at 35
◦
C.
Since it is well established that partially folded pro-
teins are less compact than fully structured proteins,
higher values of τ
R
(4, 5, 6 and 7 ns) have been
tested. It can be noted that, in the case of unfolded
proteins, the existence of multiple conformers leads
to the averaging of the diffusion anisotropy (Torchia
and Lyerla, 1974; Torchia et al., 1975; Alexandrescu
and Shortle, 1994). We have thus only considered an
isotropic overall reorientation. The best fits are ob-
tained for τ
R
equalto 5 nsand correspondingmotional
parametersare shownin Figure6. The valuesof S
2
f
as-
sociated with fast internal motions are uniformly high
along the whole protein backbone, with a mean value
of 0.76 and a standard deviation of 0.04. In contrast,
values of S
2
s
associated with slow internal motions are
much smaller with a mean value of 0.3 and a higher
standard deviation of 0.09. Higher values of S
2
s
are
found in the segment 10–50 containing A, B and C
residual helices as compared to segment 52–71. Ef-
fective internal correlation times τ
s
associated with S
2
s
are in the nanosecond range, equal to 1.12 ± 0.20 ns
in the N-terminal segment 4–50 and 0.88 ± 0.10 ns
in the C-terminal segment 51–68. The contribution of
the overall tumbling to the loss of correlation of N-H
vector motions is given by the generalized order pa-
rameter S
2
= S
2
f
S
2
s
. The low mean value of S
2
,0.23
± 0.07, indicates that the loss of correlation of N-H
vector motions is mostly due to internal motions.
Discussion
General features of the backbone dynamics in
unfolded states of proteins
The D2 domain of annexin I represents an interme-
diate state between a fully unfolded state and a fully
14
0 10203040506070
0 10203040506070
0
0.2
0.4
0.6
0.8
1
0
0.5
1
1.5
2
2.5
0
5
10
15
20
0 10203040506070
S
f
2
S
s
2
sequence
χ
2
τ
s
(ns)
A
BC E
A
BC E
(a)
(b)
(c)
Figure 6. ‘Model-free’ parameters derived from
15
N relaxation measurements obtained for the D2 domain at pH 6 and 35
◦
CusingtheMF
3
model (see Table 1) as a function of the domain sequence. The overall tumbling correlation time τ
R
is fixed at 5 ns forall residues. Bars represent
the standard deviation of simulated parameters. (a) Generalized order parameters S
2
f
(filled circles) and S
2
s
(open circles) corresponding to fast
and slow internal motions, respectively. (b) Correlation time τ
s
corresponding to slow internal motions. (c) Quality criteria of the fit as indicated
in Figure 5. Boxes at the top of the figure delineate the residual helices, gray boxes delineate the non-native turn-like structures.
folded one. Several equilibrium studies of partially
folded states of proteins obtained under mild dena-
turing conditions have shown that such states are
representative of events that transiently occur during
the kinetic folding process of the protein. A typical
study is the structural and dynamical characterization
of various unfolded states of myoglobin(Eliezer et al.,
1998). As the polypeptide chain collapses to form in-
creasing compact states, a progressive accumulation
of secondary structure associated with an increasing
restriction of backbone dynamics is observed. Restric-
tion of the backbone dynamics is directly related to
the loss of entropy during the folding process. Due
to the diversity of models used to interpret the
15
N
relaxation parameters, the comparison between the
previously published data is difficult. Nevertheless,
15
from the analysis of the spectral density values, it is
possible to clearly distinguish the dynamical behavior
of largely unfolded states from that of partially folded
polypeptide chains. Largely unfolded states contain-
ing almost no detectable residual secondary structure
such as GB1 in 7.4 M urea (Frank et al., 1995) or
SH3 in 2 M urea (Farrow et al., 1997) exhibit a flat
profile of the spectral density function along the fre-
quency dimension. For these proteins, low values of
J(0) (between 0.4 and 1.5 ns) are associated with high
values of <J(ω
H
)> (around 0.03 ns), leading to a J(0)
over <J(ω
H
)> ratio below 100 at 600 MHz. The ab-
sence of secondary structure also yields a flat profile
of the three spectral densities along the protein se-
quence, except for N- and C-terminal extremities. In
contrast, partially folded states such as lysosyme in
70% TFE (Buck et al., 1996) or the A state of ubiq-
uitin (Brutscher et al., 1997), both containing fully
stabilized secondary structure elements, exhibit large
variations of the spectral density values along the pro-
tein sequence. In the structured segments, values of
J(0) arehigherthan 4 ns and areassociated with values
of <J(ω
H
)> lower than 0.01 ns, leading to a J(0) over
<J(ω
H
)> ratio higher than 500 at 600 MHz. These
values are close to those observed in fully folded pro-
teins. Unstructured segments exhibit spectral density
values similar to those of fully unfolded proteins. In
the case of the D2 domain, the absolute values of
the spectral densities correspond to those obtained for
largely unfolded proteins with a J(0) over <J(ω
H
)>
ratioof27 and 13forthe N-terminal5–51 segmentand
for the C-terminal 52–68 segment, respectively. How-
ever, significant variations of the spectral densities
are observed along the D2 sequence. These variations
are clearly correlated with the presence of secondary
structure elements in the D2 domain that do not exist
in the fully denatured states of GB1 or SH3. Their
amplitudes remain much lower than those observed
for lysosyme in 70% TFE or the A state of ubiqui-
tin. The dynamical behavior of the D2 domain is thus
intermediate between that of a fully unfolded protein
and a partially folded state comprising fully structured
elements.
15
N relaxation data are therefore highly sen-
sitive to the degree of unfolding of partially folded
states.
Spectral densities as a probe for helical intrinsic
propensity
The examination of the spectral densities obtained for
the D2 domain highlights the typical features of resid-
ual structures. As depicted in Figure 2c, higher values
of J(ω
N
)andlowervaluesof<J(ω
H
)> are observed
in the three segments 5–13, 19–28 and 36–45. The
three segments correspond to residual helices A (4–
13), B (18–29) and C (37–44) (see residual structures
at the top of Figure2). Hence, in these residualhelices,
a lower proportion of the energy is used for motions in
the pico-second range. This is fully compatible with
the loss of flexibility of the backbone in residual he-
lices. A surprising result is that, according to chemical
shift and homonuclear NOE data, a fourth residual
helix corresponding to the native E helix (60–70) is
present. The helical population of this helix is similar
to residual A and B helices. However, this region does
not show higher values of J(ω
N
) and its dynamical
behavior is comparable to that of the quasi-disordered
segment found in place of the native D helix (50–58).
Furthermore, in the C-terminal segment comprising
the native D and E helices (50–70), values of J(0)
are significantly lower than those found in the region
spanning the A, B and C helices. This clearly indicates
that the residual E helix is characterized by a higher
flexibility in the sub-nanosecond range as compared
to A, B and C residual helices.
The singular behavior of the residual E helix can
be related to the intrinsic properties of the A and B
helices on the one hand and of the E residual helix on
the other hand, revealed by a comparison between the
entire domain and shorter isolated fragments(Cordier-
Ochsenbein et al., 1998a; Guerois et al., 1998). In a
previous work, we have shown that the helical content
of A and B helix segments is approximatelyconserved
when passing from the domain to shorter segments,
while the E helix exhibits a significantly lower helix
proportion in short fragments. The residual E he-
lix has a lower intrinsic stability and is stabilized in
the entire domain by transient long-range interactions,
most probably through non-specific hydrophobic in-
teractions (Cordier-Ochsenbein et al., 1998a). In other
words, the residual A and B helices are mostly sta-
bilized by local interactions, whereas the residual E
helix requires long-range interactions to be folded.
Interestingly, a molecular dynamics simulation per-
formed on the D2 domain showed that, along a 3 ns
trajectory, the E helix undergoes numerous helix–
turn–helix transitions while diffusing on the A and B
helix surfaces (T. Huynh, personal communication).
Altogether, our results show that the level of intrin-
sic stability of residual helices directly influences the
dynamical behavioron the sub-nanosecondtime scale.
16
Implication for protein folding
It is now well established that the balance between lo-
cal and non-local contacts markedly governs the rate
of the folding process (Alm and Baker, 1999a, b; Chiti
et al., 1999; Martinez and Serrano, 1999; Riddle et al.,
1999). Low contact orders (i.e., a high proportion
of local versus non-local interactions) lead to rapid
folding processes whereas high contact orders are as-
sociated with slower folding processes. For helical
proteins associated with low contact orders, folding is
quite well represented by a diffusion–collisionprocess
(Karplus and Weaver, 1994; Burton et al., 1998;
Munoz and Eaton, 1999; Zhou and Karplus, 1999).
Intrinsically stable helices have a high probability to
fold in the earliest stage of folding, whereas helices
with a lower intrinsic propensity are likely to be sta-
bilized concomitantly with the hydrophobic collapse.
Our analysis supports the idea that energy barriers for
helix elongation/shortening are low for helices stabi-
lized by non-local interactions such as the E helix.
This property maintains a rather low internal viscosity
and enables a rapid conformational search within the
core.
Discrete correlation times and order parameters for
unfolded proteins: The model-free approach in
question
Analysisof NMR
15
N relaxation data usingthe model-
free approach allows the evaluation of quantitative
information such as the time-scale and the relative
amplitudes of motions. However, this analysis is lim-
ited by the fact that
15
N relaxation measurement does
not provide a complete description of motions along
the protein backbone. As emphasized by LeMaster
(1999), various motions that do occur in a frequency
range higher than the highest observable NMR fre-
quency, i.e. (|ω
H
|+|ω
N
|) (180 ps at a 800 MHz field)
contribute to the relaxation rate constants but their
corresponding correlation times cannot be differenti-
ated, and a unique apparent correlation time is derived
fromthemodel-freeapproach. Conversely, all motions
slower than the lowest observable frequency, i.e. ω
N
(3.2 ns at a 500 MHz field), lead to a mean contribu-
tion to the relaxation rate constants. Motions whose
correlation times are located between these two val-
ues, (|ω
H
|+|ω
N
|) (∼180 ps) and ω
N
(∼3 ns), affect
differently each relaxation rate constant and these cor-
relation times can be differentiated. This window is
quite narrow. For fully folded proteins, this limitation
is not so restrictive since the time-scales correspond-
ing to (i) the overall tumbling of the molecule is the
main motion slower than ω
N
, (ii) possible intermedi-
ate internal motions, occurring in the sensible range
(between ω
H
+ ω
N
and ω
N
), and (iii) fast internal
motions, can reasonably be considered as a unique in-
ternal correlation time. Consequently, the model-free
approach in the case of folded proteins is appropriate
and the fitted correlation times correspond to relevant
uncorrelated motions.
The dynamical behavior of unfolded proteins is
more complex as the frequency spectrum of the dif-
ferent kinds of motion most probably corresponds to
a continuum in the pico- to nanosecond range. For
example, solving kinetic equations relative to a heli-
cal peptide leads to a nearly continuous distribution of
transition times from 0.1 ns to 10 ns associated with
the interconversion between various helical states,
such as the elongation or shortening of the helix seg-
ment by several residues or interconversions between
α, π and 3
10
helical conformations (Korzhnev et al.,
1999a, b; Orekhovet al., 1999). Withinthiscontinuum
of frequencies, it is difficult to distinguish separated
frequency ranges as opposed to the case of folded
proteins.
Considering our results obtained by applying the
model-free approach to the relaxation data of the
isolated D2 domain, we have been able to repro-
duce the experimental data with two different models,
both containing three adjustable parameters. The first
model, MF
3
, assumes that the highest correlation time
corresponds to the overall tumbling of the molecule.
The optimal value for this parameter is 5 ns (see Re-
sults). Two different internal correlation times are then
needed to reproduce experimental data, a slow effec-
tive internal motion (τ
s
) that is found around 1 ns,
and a fast effective internal motion (τ
f
) that is smaller
than 50 ps. For the second model, LMF
3
, the highest
correlation time no longer corresponds to the overall
tumbling of the molecule but rather represents a seg-
mental motion. It is adjusted independently for each
NH bond vector. We find values between 1 and 3 ns
for this local correlation time. For this second model,
fast internal motion is also needed and we find val-
ues around 80 ps. Finally, values obtained for the two
models are different and the two correlation times ob-
tained for LMF
3
lie in-between the three correlation
times obtained from the MF
3
model. Moreover, con-
sidering the variation of the parameters along the D2
sequence, linear correlationsbetween τ
s
(MF
3
)andS
2
(LMF
3
) andbetween S
2
s
(MF
3
)andτ
c
(LMF
3
) (regres-
sion coefficients of 0.74 and 0.81, respectively) are
observed. The correlated parameters, however, do not
17
have the same dimension and the same interpretation
in terms of motions. Interestingly, the profile of τ
s
(MF
3
)andS
2
(LMF
3
) along the domain sequence is
similar to that of J(ω
N
)andtheprofileofS
2
s
(MF
3
)
and τ
c
(LMF
3
) is similar to that of <J(ω
H
)>.For
model LMF
3
the presence of higher S
2
values in the
residual A, B and C helices (see Figure 5b) indicates
that the amplitude of internal motions around 80 ps
is lowered in these residual structures. This is fully
consistent with the fact that internal flexibility is hin-
dered in these segments. Conversely, for model MF
3
,
the presence of the residual A, B and C helices yields
an increase of the effective slow internal correlation
time τ
S
. This is consistent with a lower flexibility in
the nanosecond range in these residual helices.
It seems disappointing that both models fit equally
well the experimental data but lead to rather different
values of motional parameters and to two interpre-
tations in terms of motions. The experimental data
include the contribution of many correlation times,
probably a continuum, whereas each model yields
discrete values of correlation times. As emphasized
above, the optimized motional parameters represent
an averaging of several motions. For each model,
the averaging is done in a different manner, leading
to different apparent values of motional parameters
(van Heijenoort et al., 1998). The capability of the
model-free approach to provide a quantitative analy-
sis of motions in the case of unfolded proteins is thus
questionable. This also supports the idea that the for-
mer analysis of spectral density values, J(0), J(ω
N
)
and <J(ω
H
)>, is adequate for providing information
about the dynamical behavior of unfolded states such
as the D2 domain. First, it allows the distinction of
the N- and C-terminal segments according to their rel-
ative flexibility on the nanosecond time scale. Second,
the sensitivity of J(ω
N
) to motions in the nanosec-
ond range allows the discrimination of residual helices
according to their intrinsic helical propensity.
Conclusions
The variation of the spectral densities along the D2 se-
quence provides meaningful results on the conforma-
tional features of the D2 domain structure previously
depicted by chemical shift and NOE data (Cordier-
Ochsenbein et al., 1998a). The most striking result
concerns the dynamical features of residual helical
segments that are correlated with their intrinsic helical
propensity. Beside the spectral density analysis, we
showthat the model-freeapproachleads to two models
that are able to reproduce equally well our experi-
mental data within experimental error. However, these
two models provide different apparent values of order
parameters and correlation times. Our results empha-
size the difficulty to use and interpret the model-free
parameters in the case of partially or fully unfolded
proteins consisting in a wide range of inter-converting
conformers.
Acknowledgements
This work was supported by the Centre National de la
Recherche Scientifique, the Commissariat à l’Energie
Atomique and the Société de secours des amis des
sciences.
References
Alexandrescu, A.T. and Shortle, D. (1994) J. Mol. Biol., 242, 527–
546.
Alm, E. and Baker, D. (1999a) Curr. Opin. Struct. Biol., 9, 189–196.
Alm, E. and Baker, D. (1999b) Proc. Natl. Acad. Sci. USA, 96,
11305–11310.
Bewley, M.C., Boustead, C.M., Walker, J.H., Waller, D.A. and
Huber, R. (1993) Biochemistry, 32, 3923–3929.
Boyd, J. and Redfield, C. (1999) J. Am. Chem. Soc., 121, 7441–
7443.
Brutscher, B., Bruschweiler, R. and Ernst, R.R. (1997) Biochem-
istry, 36, 13043–13053.
Buck, M., Schwalbe, H. and Dobson, C.M. (1996) J. Mol. Biol.,
257, 669–683.
Burton, R.E., Myers, J.K. and Oas, T.G. (1998) Biochemistry, 37,
5337–5343.
Chiti, F., Taddei, N., White, P.M., Bucciantini, M., Magherini, F.,
Stefani, M. and Dobson, C.M. (1999) Nat. Struct. Biol., 6, 1005–
1009.
Clore, G., Szabo, A., Bax, A., Kay, L.E., Driscoll, P.C. and
Gronenborn, A.M. (1990a) J. Am. Chem. Soc., 112, 4989–4991.
Clore, G.M., Driscoll, P.C., Wingfield, P.T. and Gronenborn, A.M.
(1990b) Biochemistry, 29, 7387–7401.
Concha, N.O., Head, J.F., Kaetzel, M.A., Dedman, J.R. and Seaton,
B.A. (1993) Science, 261, 1321–1324.
Cordier-Ochsenbein, F., Cordier, S. and Russo-Marie, F. (1995)
Bio/Technology, 13, 276–278.
Cordier-Ochsenbein, F., Guerois, R., Baleux, F., Huynh-Dinh, T.,
Chaffotte, A., Neumann, J.M. and Sanson, A. (1996) Biochem-
istry, 35, 10347–10357.
Cordier-Ochsenbein, F., Guerois, R., Baleux, F., Huynh-Dinh, T.,
Lirsac, P.N., Russo-Marie, F., Neumann, J.M. and Sanson, A.
(1998a) J. Mol. Biol., 279, 1163–1175.
Cordier-Ochsenbein, F., Guerois, R., Russo-Marie, F., Neumann,
J.M. and Sanson, A. (1998b) J. Mol. Biol., 279, 1177–1185.
Dyson, H.J. and Wright, P.E. (1998) Nat. Struct. Biol., 5 (Suppl),
499–503.
Eliezer, D., Yao, J., Dyson, H.J. and Wright, P.E. (1998) Nat. Struct.
Biol., 5, 148–155.
18
Farrow, N.A., Muhandiram, R., Singer, A.U., Pascal, S.M., Kay,
C.M., Gish, G., Shoelson, S.E., Pawson, T., Forman-Kay, J.D.
and Kay, L.E. (1994) Biochemistry, 33, 5984–6003.
Farrow, N.A., Zhang, O., Forman-Kay, J.D. and Kay, L.E. (1995a)
Biochemistry, 34, 868–878.
Farrow, N.A., Zhang, O., Forman-Kay, J.D. and Kay, L.E. (1997)
Biochemistry, 36, 2390–2402.
Farrow, N.A., Zhang, O., Szabo, A., Torchia, D.A. and Kay, L.E.
(1995b) J. Biomol. NMR, 6, 153–162.
Frank, M.K., Clore, G.M. and Gronenborn, A.M. (1995) Protein
Sci., 4, 2605–2615.
Grzesiek, S. and Bax, A. (1993) J. Am. Chem. Soc., 115, 12593–
12594.
Guerois, R., Cordier-Ochsenbein, F., Baleux, F., Huynh-Dinh, T.,
Neumann, J.M. and Sanson, A. (1998) Protein Sci., 7, 1506–
1515.
Huber, R., Berendes, R., Burger, A., Schneider, M., Karshikov, A.,
Luecke, H., Romisch, J. and Paques, E. (1992) J. Mol. Biol., 223,
683–704.
Ishima, R. and Nagayama, K. (1995) Biochemistry, 34, 3162–3171.
Ishima, R. and Torchia, D.A. (2000) Nat. Struct. Biol., 7, 740–743.
Ishima, R., Yamasaki, K., Saito, M. and Nagayama, K. (1995) J.
Biomol. NMR, 6, 217–220.
Karplus, M. and Weaver, D.L. (1994) Protein Sci., 3, 650–668.
Kay, L.E., Torchia, D.A. and Bax, A. (1989) Biochemistry, 28,
8972–8979.
Korzhnev, D.M., Orekhov, V.Y. and Arseniev, A.S. (1999a) J.
Biomol. NMR, 14, 357–368.
Korzhnev, D.M., Orekhov, V.Y., Arseniev, A.S., Gratias, R. and
Kessler, H. (1999b) J. Phys. Chem., B103, 7036–7043.
Kraulis, P.J. (1991) J. Appl. Crystallogr., 24, 946–950.
Lefevre, J.F., Dayie, K.T., Peng, J.W. and Wagner, G. (1996)
Biochemistry, 35, 2674–2686.
LeMaster, D.M. (1999) J. Am. Chem. Soc., 121, 1726–1742.
Lipari, G. and Szabo, A. (1982a) J. Am. Chem. Soc., 104, 4546–
4559.
Lipari, G. and Szabo, A. (1982b) J. Am. Chem. Soc., 104, 4559–
4570.
Mandel, A.M., Akke, M. and Palmer III, A.G. (1995) J. Mol. Biol.,
246, 144–163.
Marion, D., Kay, L.E., Sparks, S.W., Torchia, D.A. and Bax, A.
(1989) J. Am. Chem. Soc., 111, 1515–1517.
Martinez, J.C. and Serrano, L. (1999) Nat. Struct. Biol., 6, 1010–
1016.
Meekhof, A.E. and Freund, S.M. (1999) J. Mol. Biol., 286, 579–
592.
Munoz, V. and Eaton, W.A. (1999) Proc. Natl. Acad. Sci. USA, 96,
11311–11316.
Orekhov, V.Y., Korzhnev, D.M., Diercks, T., Kessler, H. and
Arseniev, A.S. (1999) J. Biomol. NMR, 14, 345–356.
Palmer III, A.G., Rance, M. and Wright, P.E. (1991) J. Am. Chem.
Soc., 113, 4371–4380.
Peng, J.W. and Wagner, G. (1992a) Biochemistry, 31, 8571–8586.
Peng, J.W. and Wagner, G. (1992b) J. Magn. Reson., 98, 308–332.
Peng, J.W. and Wagner, G. (1995) Biochemistry, 34, 16733–16752.
Phan, I.Q.H., Boyd, J. and Campbell, I.D. (1996) J. Biomol. NMR,
8, 369–378.
Piotto, M., Saudek, V. and Sklenar, V. (1992) J. Biomol. NMR, 2,
661–665.
Pons, J.L., Malliavin, T.E. and Delsuc, M.A. (1996) J. Biomol.
NMR, 8, 445–552.
Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T.
(1988) Numerical Recipes in C – The Art of Scientific Comput-
ing, Cambridge University Press, Cambridge, U.K.
Riddle, D.S., Grantcharova, V.P., Santiago, J.V., Alm, E., Ruczinski,
I. and Baker, D. (1999) Nat. Struct. Biol., 6, 1016–1024.
Rouh, A., Delsuc, M.A., Bertrand, G. and Lallemand, J.Y. (1993) J.
Magn. Reson., 102, 357–359.
Schwalbe, H., Fiebig, K.M., Buck, M., Jones, J.A., Grimshaw, S.B.,
Spencer, A., Glaser, S.J., Smith, L.J. and Dobson, C.M. (1997)
Biochemistry, 36, 8977–8991.
Shaka, A.J., Barker, P.B. and Freeman, R. (1985) J. Magn. Reson.,
64, 547–552.
Torchia, D.A. and Lyerla Jr., J.R. (1974) Biopolymers, 13, 97–114.
Torchia, D.A., Lyerla Jr., J.R. and Quattrone, A.J. (1975) Biochem-
istry, 14, 887–900.
van Heijenoort, C., Penin, F. and Guittet, E. (1998) Biochemistry,
37, 5060–5073.
Weng, X., Luecke, H., Song, I.S., Kang, D.S., Kim, S.H. and Huber,
R. (1993) Protein Sci., 2, 448–458.
Zhou, Y. and Karplus, M. (1999) Nature, 401, 400–403.