Figure 1 - uploaded by Gloria E O Borgstahl
Content may be subject to copyright.
Source publication
Recent challenges in biological X-ray crystallography include the processing of modulated diffraction data. A modulated crystal has lost its three-dimensional translational symmetry but retains long-range order that can be restored by refining a periodic modulation function. The presence of a crystal modulation is indicated by an X-ray diffraction...
Contexts in source publication
Context 1
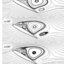
... modulated crystals can have satellite reflections in more than one direction, requiring multiple q vectors. In the example illustrated in Fig. 1( c ), q 1 and q 2 differ in direction as well as spacing between the satellites and mains and can be expressed ...
Context 2
... The positions of the satellite reflections are therefore defined by the q vector 4 For the example in Fig. 1( a ), there is a single modulation vector with single- order satellites that are parallel to b * with values of m = ( Æ 1, 0). In this case, (4) then reduces to q 1⁄4 0 a à þ q b à þ 0 c à : ð 5 Þ Of course, a modulation wave does not have to be parallel to one of the reciprocal basis vectors. Instead, in more complicated cases two or three of the scalar q coefficients in (5) can be non- zero. Furthermore, if the change in structure owing to the modulation is large, multiple-order satellites can exist. In such cases, to index the multiple- order satellites, the q vector repre- senting the elementary displacement from a main reflection would be multi- plied by integer values of m ranging beyond À 1 to 1. Fig. 1( b ) illustrates a case in which m ranges from À 2 to 2 and the single q vector has the ...
Context 3
... The positions of the satellite reflections are therefore defined by the q vector 4 For the example in Fig. 1( a ), there is a single modulation vector with single- order satellites that are parallel to b * with values of m = ( Æ 1, 0). In this case, (4) then reduces to q 1⁄4 0 a à þ q b à þ 0 c à : ð 5 Þ Of course, a modulation wave does not have to be parallel to one of the reciprocal basis vectors. Instead, in more complicated cases two or three of the scalar q coefficients in (5) can be non- zero. Furthermore, if the change in structure owing to the modulation is large, multiple-order satellites can exist. In such cases, to index the multiple- order satellites, the q vector repre- senting the elementary displacement from a main reflection would be multi- plied by integer values of m ranging beyond À 1 to 1. Fig. 1( b ) illustrates a case in which m ranges from À 2 to 2 and the single q vector has the ...
Similar publications
Amyotrophic lateral sclerosis (ALS) is a late-onset neurodegenerative disorder resulting from motor neuron death. Approximately 10% of cases are familial (FALS), typically with a dominant inheritance mode. Despite numerous advances in recent years, nearly 50% of FALS cases have unknown genetic aetiology. Here we show that mutations within the profi...
One of the most significant biosphere contamination problems worldwide is derived from heavy metals. Heavy metals can be highly reactive and toxic according to their oxidation levels. Their toxic effects are associated with the increased production of reactive oxygen species (ROS) and cellular damage induced in plants. The present study focuses on...
Bu çalışmada, ince bir füze kanadının sabit hızlı ses-üstü uçuş koşulunda ve farklı hücum açılarındaki hesaplamalı akışkanlar dinamiği analizleri yapılmıştır. Yapılan analizler sonucu, kanada etkiyen maksimum kuvvet girdi olarak kabul edilerek yapısal analiz gerçekleştirilmiştir. Çalışmada, deniz seviyesinden 1000 m yükseklikteki uçuş değerleri göz...
Citations
... Regarding the first question, on the one hand, we must distinguish between macromolecular (such as DNA molecules and protein complexes) or supramolecular (e.g., protein and virus crystals) condensed matter phases, and cellular ensembles in biological tissues, on the other hand. For one thing, the existence of a number of protein based aperiodic crystals, belonging to the incommensurate modulated phase class, has been well documented from the detailed study of their obtained x-ray diffraction data during the last decade [90][91][92][93][94]. On the contrary, the possible application of diffraction techniques to characterize the order underlying in biological tissues is a delicate issue. ...
Biological systems display a broad palette of hierarchically ordered designs spanning over many orders of magnitude in size. Remarkably enough, periodic order, which profusely shows up in nonliving ordered compounds, plays a quite subsidiary role in most biological structures, which can be appropriately described in terms of the more general aperiodic crystal notion instead. In this Topical Review I shall illustrate this issue by considering several representative examples, including botanical phyllotaxis, the geometry of cell patterns in tissues, the morphology of sea urchins, or the symmetry principles underlying virus architectures. In doing so, we will realize that albeit the currently adopted quasicrystal notion is not general enough to properly account for the rich structural features one usually finds in biological arrangements of matter, several mathematical tools and fundamental notions belonging to the aperiodic crystals science toolkit can provide a useful modeling framework to this end.
... Regarding the first question, on the one hand, we must distinguish between macromolecular (such as DNA molecules and protein complexes) or supramolecular (e. g., protein and virus crystals) condensed matter phases, and cellular ensembles in biological tissues, on the other hand. For one thing, the existence of a number of protein based aperiodic crystals, belonging to the incommensurate modulated phase class, has been well documented from the detailed study of their obtained X-ray diffraction data during the last decade [90][91][92][93][94]. On the contrary, the possible application of diffraction techniques to characterize the order underlying in biological tissues is a delicate issue. ...
Biological systems display a broad palette of hierarchically ordered designs spanning over many orders of magnitude in size. Remarkably enough, periodic order, which profusely shows up in non-living ordered compounds, plays a quite subsidiary role in most biological structures, which can be appropriately described in terms of the more general aperiodic crystal notion instead. In this Topical Review I shall illustrate this issue by considering several representative examples, including botanical phyllotaxis, the geometry of cell patterns in tissues, the morphology of sea urchins, or the symmetry principles underlying virus architectures. In doing so, we will realize that albeit the currently adopted quasicrystal notion is not general enough to properly account for the rich structural features one usually finds in biological arrangements of matter, several mathematical tools and fundamental notions belonging to the aperiodic crystals science toolkit can provide a useful modeling framework to this end.
... The indexing indicated an orthorhombic space group with a single q vector required to describe the modulated reflections based on the superspace theory developed by Janner and Janssen [21][22][23]. A few years later Porta and coworkers were able to collect, index, and integrate a complete cryocooled modulated dataset of PA [49] using Eval15 [50]. They also performed simulations to work out approaches to refine these types of structures [51][52][53]. ...
... It is very powerful but, in our experience, has steep learning curve, when compared to some of the other programmes, but Eval15 has been able to index and integrate data that other programmes cannot. For example, it has successfully indexed and integrated multiple incommensurately modulated protein datasets [49,54]. ...
... The other category is incommensurate where an integer number of unit cells do not line up with the modulation period. Figure 27 shows a one-dimensional displacement modulation with the modulation function overlaid on the unit cells [49]. In the periodic case, the protein is in the same position in consecutive unit cells (Figure 27(a)). ...
Macromolecular crystal structure determination can be complicated or brought to a halt by crystal imperfections. These issues motivated us to write up what we affectionately call ‘The Definitive Hitchhiker’s Guide to Pathological Macromolecular Crystals: Lattice Disorders and Modulations’. Perhaps the most challenging imperfections are lattice order–disorder phenomena and positional modulations. Many of these types of crystals have been solved, and progress has been made on the more challenging forms. Diagnostic tools and how to solve many of these problem crystal structures are reviewed. New avenues are provided for approaching the solution of incommensurately modulated crystals. There are a good number of case studies in the literature of lattice order–disorder phenomena and crystallographic modulations that make it timely to write a review. This review concludes with a projected pathway for solving incommensurately modulated crystals, personal views of future directions and needs of the crystallographic community.
... Another type of deviation from perfect periodicity in a crystal, is crystal modulation, in which the content of asymmetric unit is not perfectly replicated by the lattice operations and which can occur with a period commensurate or incommensurate with the lattice periodicity. As result of crystal modulation, primary Bragg reflections are flanked by off-lattice satellite reflections 10 . The direction and magnitude of such satellite reflections is described by an additional vector q, which needs to be added to the reciprocal space vector H to define a 4-dimensional reciprocal space vector. ...
... The direction and magnitude of such satellite reflections is described by an additional vector q, which needs to be added to the reciprocal space vector H to define a 4-dimensional reciprocal space vector. Although incommensurate crystals have been reported rarely in macromolecular protein crystallography 11,12 , the EVAL software suite can index and process such data 10,13 , and in silico simulations of modulated structure have been performed 14 . ...
Abstract Twinning is a crystal growth anomaly, which has posed a challenge in macromolecular crystallography (MX) since the earliest days. Many approaches have been used to treat twinned data in order to extract structural information. However, in most cases it is usually simpler to rescreen for new crystallization conditions that yield an untwinned crystal form or, if possible, collect data from non-twinned parts of the crystal. Here, we report 11 structures of engineered variants of the E. coli enzyme N-acetyl-neuraminic lyase which, despite twinning and incommensurate modulation, have been successfully indexed, solved and deposited. These structures span a resolution range of 1.45–2.30 Å, which is unusually high for datasets presenting such lattice disorders in MX and therefore these data provide an excellent test set for improving and challenging MX data processing programs.
... Modulated structures are relatively well known in small-molecule crystallography [21] but in protein crystallography are almost unheard of (probably because such cases, even if encountered, were discarded in the past as too difficult) although attempts have been made to investigate them methodically [22,23]. In cases of incommensurate modulation even the data processing [24] might be an insurmountable problem. One of the few successfully tackled modulated protein crystal structures is that of the plant protein Hyp-1 in complex with the fluorescent dye ANS, which was successfully solved by molecular replacement with tNCS-adjusted maximum-likelihood targets [25] and described as a tetartohedrally twinned commensurate phase with seven-fold expanded unit cell containing 28 independent protein molecules [26]. ...
Macromolecules, such as proteins or nucleic acids, form crystals with a large volume fraction of water, ~50% on average. Apart from typical physical defects and rather trivial poor quality problems, macromolecular crystals, as essentially any crystals, can also suffer from several kinds of pathologies, in which everything seems to be perfect, except that from the structural point of view the interpretation may be very difficult, sometimes even impossible. A frequent nuisance is pseudosymmetry, or non-crystallographic symmetry (NCS), which is particularly nasty when it has translational character. Lattice-translocation defects, also called order-disorder twinning (OD-twinning), occur when molecules are packed regularly in layers but the layers are stacked (without rotation) in two (or more) discrete modes, with a unique translocation vector. Crystal twinning arises when twin domains have different orientations, incompatible with the symmetry of the crystal structure. There are also crystals in which the periodic (lattice) order is broken or absent altogether. When the strict short-range translational order from one unit cell to the next is lost but the long-range order is restored by a periodic modulation, we have a modulated crystal structure. In quasicrystals (not observed for macromolecules yet), the periodic order (in 3D space) is lost completely and the diffraction pattern (which is still discrete) cannot be even indexed using three hkl indices. In addition, there are other physical defects and phenomena (such as high mosaicity, diffraction anisotropy, diffuse scattering, etc.) which make diffraction data processing and structure solution difficult or even impossible.
Indexing is usually simple when positions of diffraction peaks are sufficiently accurate, but for some crystals, complications arise even if the positions are free from errors. Below, selected departures from simple crystal indexing are described. The chapter comprises short accounts on the mutually related subjects of pseudosymmetry which arises in structure determination, diffraction by twins and ambiguities in diffraction-based orientation determination. Moreover, the chapter includes sections on modulated structures and on indexing data from non-conventional experimental diffraction methods.
Two commensurately modulated structures (PDB entries 4n3e and 6sjj) were solved using translational noncrystallographic symmetry (tNCS). The data required the use of large supercells, sevenfold and ninefold, respectively, to properly index the reflections. Commensurately modulated structures can be challenging to solve. Molecular-replacement software such as Phaser can detect tNCS and either handle it automatically or, for more challenging situations, allow the user to enter a tNCS vector, which the software then uses to place the components. Although this approach has been successful in solving these types of challenging structures, it does not make it easy to understand the underlying modulation in the structure or how these two structures are related. An alternate view of this problem is that the atoms and associated parameters are following periodic atomic modulation functions (AMFs) in higher dimensional space, and what is being observed in these supercells are the points where these higher dimensional AMFs intersect physical 3D space. In this case, the two 3D structures, with a sevenfold and a ninefold superstructure, seem to be quite different. However, describing those structures within the higher dimensional superspace approach makes a strong case that they are closely related, as they show very similar AMFs and can be described with one unique (3+1)D structure, i.e. they are two different 3D intersections of the same (3+1)D structure.
Superstructure modulation, with violation of the strict short-range periodic order of consecutive crystal unit cells, is well known in small-molecule crystallography but is rarely reported for macromolecular crystals. To date, one modulated macromolecular crystal structure has been successfully determined and refined for a pathogenesis-related class 10 protein from Hypericum perforatum (Hyp-1) crystallized as a complex with 8-anilinonaphthalene-1-sulfonate (ANS) [Sliwiak et al. (2015), Acta Cryst. D 71 , 829–843]. The commensurate modulation in that case was interpreted in a supercell with sevenfold expansion along c . When crystallized in the additional presence of melatonin, the Hyp-1–ANS complex formed crystals with a different pattern of structure modulation, in which the supercell shows a ninefold expansion of c , manifested in the diffraction pattern by a wave of reflection-intensity modulation with crests at l = 9 n and l = 9 n ± 4. Despite complicated tetartohedral twinning, the structure has been successfully determined and refined to 2.3 Å resolution using a description in a ninefold-expanded supercell, with 36 independent Hyp-1 chains and 156 ANS ligands populating the three internal (95 ligands) and five interstitial (61 ligands) binding sites. The commensurate superstructures and ligand-binding sites of the two crystal structures are compared, with a discussion of the effect of melatonin on the co-crystallization process.
Theoretically, crystals with supercells exist at a unique crossroads where they can be considered as either a large unit cell with closely spaced reflections in reciprocal space or a higher dimensional superspace with a modulation that is commensurate with the supercell. In the latter case, the structure would be defined as an average structure with functions representing a modulation to determine the atomic location in 3D space. Here, a model protein structure and simulated diffraction data were used to investigate the possibility of solving a real incommensurately modulated protein crystal using a supercell approximation. In this way, the answer was known and the refinement method could be tested. Firstly, an average structure was solved by using the `main' reflections, which represent the subset of the reflections that belong to the subcell and in general are more intense than the `satellite' reflections. The average structure was then expanded to create a supercell and refined using all of the reflections. Surprisingly, the refined solution did not match the expected solution, even though the statistics were excellent. Interestingly, the corresponding superspace group had multiple 3D daughter supercell space groups as possibilities, and it was one of the alternate daughter space groups that the refinement locked in on. The lessons learned here will be applied to a real incommensurately modulated profilin–actin crystal that has the same superspace group.