Fig 4 - uploaded by Samir Adly
Content may be subject to copyright.
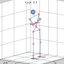
Zener diode model. current or input voltage. There is a current point I 1 , called the Zener knee current, which is the minimum value of the Zener current required to maintain voltage regulation and a maximum allowable value of Zener current I 2. Currents above this value will damage or destroy the model.
Source publication
In this paper, we show how the approach of Moreau and Panagiotopoulos can be used to develop a suitable method for the formulation and mathematical analysis of circuits involving devices like diodes and thyristors.
Context in source publication
Context 1
... 4. The Zener diodes are made to permit current to flow in the reverse direction if the voltage is larger then the rated breakdown or "Zener voltage" V 2 . For example, for a practical diode, V 1 0.7 V and V 2 = −7 V. The Zener diode is (see Fig. 4) a good voltage regulator for maintaining a constant voltage regardless of minor variations in load current or input voltage. There is a current point I 1 , called the Zener knee current, which is the minimum value of the Zener current required to maintain voltage regulation and a maximum allowable value of Zener current I 2 . Currents ...
Similar publications
A complex solution of problem of creating mathematical models of multi-energy systems is possible using a unified approach. An approach that will ensure consistent construction of mathematical models and unification of computational algorithms. The paper presents the elements of the concept of energy circuits as a basis for unified modeling of syst...
Citations
... The presented nonsmooth formalism can be seen as one form of the classical hydraulic-electric analogy [1][2][3][4], and it is also analogous to the nonsmooth electronics [19][20][21]. From another perspective, the presented approach is close to those of some previous papers [22][23][24] that apply the singular perturbation theory to the dynamical models of hydraulic systems. ...
This paper presents an analytical approach for modeling the quasistatic characteristics of hydraulic actuators driven by four-valve independent metering circuits. The presented model is described as a nonsmooth, set-valued function from the velocity to the set of forces with which the equilibrium is achieved at the velocity. It is derived from algebraic relations among the velocity of the actuator, the steady-state force generated by the actuator, and the flowrate and the steady-state pressure at all valves in the circuit. This approach is also applied to more involving circuits including a regeneration pipeline and those with multiple actuators. The contribution of the paper can be seen as an example case study of the fact that these complicated circuit structures are analytically tractable through an extension of the conventional hydraulic-electric analogy. The obtained analytical expressions of the steady-state velocity-force relations allow for concise visualization of the actuators' characteristics.
... Modeling of electrical circuits has attracted much interest over the past few decades and it has been studied in numerous articles and books [1,3,4]. The following framework has been proposed in [2]. ...
... Today, it remains an object of mathematical research. Significant applications of sweeping processes have been given, specifically in electrical circuits [1,3,7], crowd motion modeling [113,112], hysteresis in elastoplastic models [99], mathematical economics [62,75], dynamic networks, nonsmooth mechanics [100] and many other. The sweeping process theory has become an important area of nonlinear and variational analysis ...
This thesis deals with analysis of constrained dynamical systems, supported by some numerical methods. The systems that we consider can be broadly seen as a class of nonsmooth systems, where the state trajectory is constrained to evolve within a prespecified (and possibly time-varying) set. The possible discontinuities in these systems arise due to sudden change in the vector field at the boundary of the constraint set. The general framework that we adopt has been linked to different classes of nonsmooth systems in the literature, and it can be described by an interconnection of an ordinary differential equation with a static relation (such as variational inequality, or a normal cone inclusion, or complementarity relations). Such systems have found applications in modeling of several engineering and physical systems, and the results of this dissertation make some contributions to the analysis and numerical methods being developed for such system class.
The first problem that we consider is related to the stability of an equilibrium point for the aforementioned class of nonsmooth systems. We provide appropriate definitions for stability of an equilibrium, and the Lyapunov functions, which take into consideration the presence of constraints in the system. In the presence of conic constraints, it seems natural to work with cone-copositive Lyapunov functions. To confirm this intuition, and as the first main result, we prove that, for a certain class of cone-constrained systems with an exponentially stable equilibrium, there always exists a smooth cone-copositive Lyapunov function. Putting some more structure on the system vector field, such as homogeneity, we can show that the aforementioned functions can be approximated by a rational function of cone-copositive homogeneous polynomials.
This later class of functions is seen to be particularly amenable for numerical computation as we provide two types of algorithms precisely for that purpose. These algorithms consist of a hierarchy of either linear or semidefinite optimization problems for computing the desired cone-copositive Lyapunov function. For conic constraints, we provide a discretization algorithm based on simplicial partitioning of a simplex, so that the search of the desired function is addressed by constructing a hierarchy (associated with the diameter of the cells in the partition) of linear programs. Our second algorithm is tailored to semi-algebraic sets, where a hierarchy of semidefinite programs is constructed to compute Lyapunov functions as a sum of squares of polynomials. Some examples are given to illustrate our approach.
Continuing with our study of state-constrained systems, we next consider the time evolution of a probability measure which describes the distribution of the state over a set. In contrast with smooth ordinary differential equations, where the evolution of this probability measure is described by the Liouville equation, the flow map associated with the nonsmooth differential inclusion is not necessarily invertible and one cannot directly derive a continuity equation to describe the evolution of the distribution of states. Instead, we consider Lipschitz approximation of our original nonsmooth system and construct a sequence of measures obtained from Liouville equations corresponding to these approximations. This sequence of measures converges in weak-star topology to the measure describing the evolution of the distribution of states for the original nonsmooth system. This allows us to approximate numerically the evolution of moments (up to some finite order) for our original nonsmooth system, using a hierarchy of semidefinite programs. Using similar methodology, we study the approximation of the support of the solution (described by a measure at each time) using polynomial approximations.
... Modeling of electrical circuits has attracted much interest over the past few decades and it has been studied in numerous articles and books [1,3,4]. The following framework has been proposed in [2]. ...
... Today, it remains an object of mathematical research. Significant applications of sweeping processes have been given, specifically in electrical circuits [1,3,7], crowd motion modeling [113,112], hysteresis in elastoplastic models [99], mathematical economics [62,75], dynamic networks, nonsmooth mechanics [100] and many other. The sweeping process theory has become an important area of nonlinear and variational analysis ...
This thesis deals with analysis of constrained dynamical systems, supported by some numerical methods. The systems that we consider can be broadly seen as a class of nonsmooth systems, where the state trajectory is constrained to evolve within a prespecified (and possibly time-varying) set. The possible discontinuities in these systems arise due to sudden change in the vector field at the boundary of the constraint set. The general framework that we adopt has been linked to different classes of nonsmooth systems in the literature, and it can be described by an interconnection of an ordinary differential equation with a static relation (such as variational inequality, or a normal cone inclusion, or complementarity relations). Such systems have found applications in modeling of several engineering and physical systems, and the results of this dissertation make some contributions to the analysis and numerical methods being developed for such system class.
The first problem that we consider is related to the stability of an equilibrium point for the aforementioned class of nonsmooth systems. We provide appropriate definitions for stability of an equilibrium, and the Lyapunov functions, which take into consideration the presence of constraints in the system. In the presence of conic constraints, it seems natural to work with cone-copositive Lyapunov functions. To confirm this intuition, and as the first main result, we prove that, for a certain class of cone-constrained systems with an exponentially stable equilibrium, there always exists a smooth cone-copositive Lyapunov function. Putting some more structure on the system vector field, such as homogeneity, we can show that the aforementioned functions can be approximated by a rational function of cone-copositive homogeneous polynomials.
This later class of functions is seen to be particularly amenable for numerical computation as we provide two types of algorithms precisely for that purpose. These algorithms consist of a hierarchy of either linear or semidefinite optimization problems for computing the desired cone-copositive Lyapunov function. For conic constraints, we provide a discretization algorithm based on simplicial partitioning of a simplex, so that the search of the desired function is addressed by constructing a hierarchy (associated with the diameter of the cells in the partition) of linear programs. Our second algorithm is tailored to semi-algebraic sets, where a hierarchy of semidefinite programs is constructed to compute Lyapunov functions as a sum of squares of polynomials. Some examples are given to illustrate our approach.
Continuing with our study of state-constrained systems, we next consider the time evolution of a probability measure which describes the distribution of the state over a set. In contrast with smooth ordinary differential equations, where the evolution of this probability measure is described by the Liouville equation, the flow map associated with the nonsmooth differential inclusion is not necessarily invertible and one cannot directly derive a continuity equation to describe the evolution of the distribution of states. Instead, we consider Lipschitz approximation of our original nonsmooth system and construct a sequence of measures obtained from Liouville equations corresponding to these approximations. This sequence of measures converges in weak-star topology to the measure describing the evolution of the distribution of states for the original nonsmooth system. This allows us to approximate numerically the evolution of moments (up to some finite order) for our original nonsmooth system, using a hierarchy of semidefinite programs. Using similar methodology, we study the approximation of the support of the solution (described by a measure at each time) using polynomial approximations.
... They were introduced in the seminal paper [14] by J.J. Moreau in the context of plasticity and friction theory. Since then, there has been an increasing interest in sweeping systems with its range of application covering now problems from mechanics, engineering, economics and crowd motion problems; see, for example, [1], [5], [12], [13], [17] and [9]. ...
... Assuming that the set C in (1) is time independent, necessary conditions in the form of a maximum principle for optimal control problems involving such systems are derived in [2], [4] and [9]. A special feature of [9] is that it relies on an approximating sequence of optimal control problems differing from the original problem insofar as (1) CONTACT G. Smirnov. Email: smirnov@math.uminho.pt is replaced by a differential equation of the forṁ x γk (t) = f (t, x γk (t), u(t)) − γ k e γkψ(xγ k (t)) ∇ψ(x γk (t)) (2) for some positive sequence γ k → +∞. ...
We generalize the Maximum Principle for free end point optimal control problems involving sweeping systems derived in [9] to cover the case where the end point is constrained to take values in a certain set. As in [9], an ingenious smooth approximating family of standard differential equations plays a crucial role.
... The presented formalism can be said to be close to the classical hydraulic-electric analogy [10,12], which replaces the pressure and the flowrate by the voltage and the current, respectively. Considering that the presented approach involves the nonsmoothness, it is also analogous to the nonsmooth electronics [1,3,11]. In this analogy, a check valve, for example, corresponds to an ideal diode [1]. ...
This article presents a quasistatic model of a hydraulic actuator driven by a four-valve independent metering circuit. The presented model describes the quasistatic balance between the velocity and force and that between the flowrate and the pressure. In such balanced states, the pressure difference across each valve determines the oil flowrate through the valve, the oil flowrate into the actuator determines the velocity of the actuator, and the pressures in the actuator chambers are algebraically related to the external force acting on the actuator. Based on these relations, we derive a set of quasistatic representations, which analytically relates the control valve openings, the actuator velocity, and the external force. This analytical expression is written with nonsmooth functions, of which the return values are set-valued instead of single-valued. We also show a method of incorporating the obtained nonsmooth quasistatic model into multibody simulators, in which a virtual viscoelastic element is used to mimic transient responses. In addition, the proposed model is extended to include a regeneration pipeline and to deal with a collection of actuators driven by a single pump.
... Moreau was originally motivated by plasticity and friction dynamics (cf. [49,52,54]), but now sweeping processes have found applications to nonsmooth mechanics (see, e.g., [45,37,55]), to economics (cf., e.g., [30,23,28]), to electrical circuits (see, e.g., [2,9,1,3]), to crowd motion modeling (cf., e.g., [42,39,43,41,40,24]), and to other fields (see, e.g., the references in the recent paper [65]). The theoretical analysis of problem (1.4)-(1.7) ...
... We start by proving the uniqueness of solutions to (3.1)-(3.5) in Theorem 3.1. 2 is nonincreasing and leads to the uniqueness of the solution since y i (t) = Proj C(t) (y i (t−)) and y i (t+) = Proj C(t+) (y i (t−)) for i = 1, 2. ...
In this paper we provide a formulation for sweeping processes with arbitrary locally bounded retraction, not necessarily left or right continuous. Moreover we provide a proof of the existence and uniqueness of solutions for this formulation which relies on the reduction to the $1$-Lipschitz continuous case by using a suitable family of geodesics for the asymmetric Hausdorff-like distance called "excess".
... The unique aspect of such systems is the presence of the normal cone, which produces differential inclusions with unbounded and discontinuous right-hand side. These systems first appear in the literature as a framework to study the dynamics of plasticity and friction in the paper [1] by J.J. Moreau of sweeping systems range from mechanics to crowd motion modelling; see, for example, [2][3][4][5][6]. Not surprisingly, we have also witnessed an increasing interest in optimal control problems involving these systems; see, for example, [3,4,[7][8][9][10][11][12] and references therein. ...
... Suppose now that x 0 = y 0 . Taking into account the definition of γ (see (2)), and the fact that ψ(y) ≤ −ξ (by Lemma 3.1), we conclude from (8) that ...
This paper focuses on numerical methods for a class of optimal control problems involving sweeping processes. We consider a problem, where the sweeping set is constant and coincides with the 0 level set of a C2\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$C^2$$\end{document} convex function. For such problems, we propose a numerical method based on a sequence of approximating standard optimal control problems. We illustrate our method treating numerically an example.
... The original concrete motivations of the sweeping process by J.J. Moreau are the study of quasi-static evolution in elastoplasticity [11]. Nowadays, many models in nonsmooth mechanics, mathematical economics, simulation of switched electrical circuits and crowd motion can be formulated by the sweeping process approach (for more details, we refer to [1,3,4,2,7,8,10,12] and references therein). ...
... Consequently, u is a solution of (2) with the initial value u(0) = 0. The aim of the present paper is to show how a fixed point approach can lead to the existence theorem for the implicit differential inclusion described by (2). By using Schauder's fixed point theorem and the existence and uniqueness theorem for the problem (2) with time-dependent C (i.e. ...
... In section 2 we introduce some notations and state some preliminary results needed throughout the paper. In section 3, we present an existence theorem related to problem (2). A uniqueness result for the particular case of a shifted moving set is discussed in section 4. Section 5 is devoted to some concluding remarks and open questions. ...
In this paper, we study a variant of the state-dependent sweeping process with velocity constraint. The constraint
C
(
⋅
,
u
)
C(⋅,u) depends upon the unknown state
u
u, which causes one of the main difficulties in the mathematical treatment of quasi-variational inequalities. Our aim is to show how a fixed point approach can lead to an existence theorem for this implicit differential inclusion. By using Schauder's fixed point theorem combined with a recent existence and uniqueness theorem in the case where the moving set
C
C does not depend explicitly on the state
u
u (i.e.
C
:=
C
(
t
)
C:=C(t)) given in [4], we prove a new existence result of solutions of the quasi-variational sweeping process in the infinite dimensional Hilbert spaces with a velocity constraint. Contrary to the classical state-dependent sweeping process, no conditions on the size of the Lipschitz constant of the moving set, with respect to the state, is required.
... for some function ψ : R n → R with ψ(0) < 0. 1 We say that a pair (x, u) is an admissible process for (P ) when x is an absolutely continuous function and u is a measurable function satisfying the constraints of (P ). ...
... Rights reserved. 1] |x(t)| ≤ |x 0 | + M 2 + 2 ( 8 ) ...
We present existence of solution and necessary conditions for an optimal control problem with a particular case of sweeping processes with constant sweeping set. Using a sequence of approximating problems we prove existence of solution and necessary conditions. The special feature of our approach resides on the nature of the approximating problems: in contrast with other literature these problems do not rely on distance functions to the sweeping set.
... Such functions ϕ i are related to the so-called convex or nonconvex superpotentials, and their subdifferential ∂ϕ i represents constitutive mechanical laws or voltage-current characteristics of some electrical devices (diodes, DIAC, transistors, etc.). We refer the reader to [1,2,[6][7][8] for more details. ...
... • Convex superpotential In order to deal with nonlinear phenomena like unilateral contact and Coulomb friction, the notion of superpotential has been introduced by J.J. Moreau [9] in 1968 for convex, not necessarily differentiable, energy functionals. We say that the forces f derive from Moreau's superpotential if the function ϕ : X → R is proper, closed and convex, i.e., ϕ ∈ 0 (X) and∂ = ∂ coincides with the convex subdifferential defined in (6). In this case, the equilibrium equation (10) is linked to the theory of variational inequalities, since ...
... , m. The inclusion p i (t) ∈∂ϕ i (q i (t)) may represent the voltage-current characteristics of some electronic devices or some constitutive laws in mechanical systems [1,2,6,7,12]. It is easy to see that (26) can be rewritten as: ...
The main concern of this paper is to investigate the Lipschitzian-like stability property (namely Aubin property) of the solution map of possibly nonmonotone variational systems with composite superpotentials. Using Mordukhovich coderivative criterion and a second-order subdifferential analysis, we provide simple and verifiable characterizations of this property in terms of the data involved in the problem. Applications are given in nonsmooth mechanics. © 2018 Springer Science+Business Media, LLC, part of Springer Nature